Algebra Formula Collection, Perfect Algebra Formula Collection

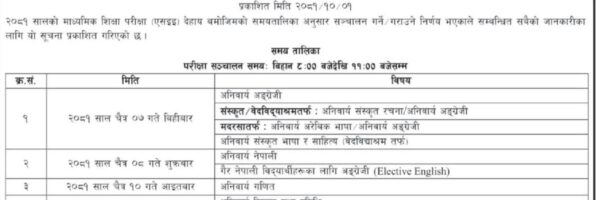
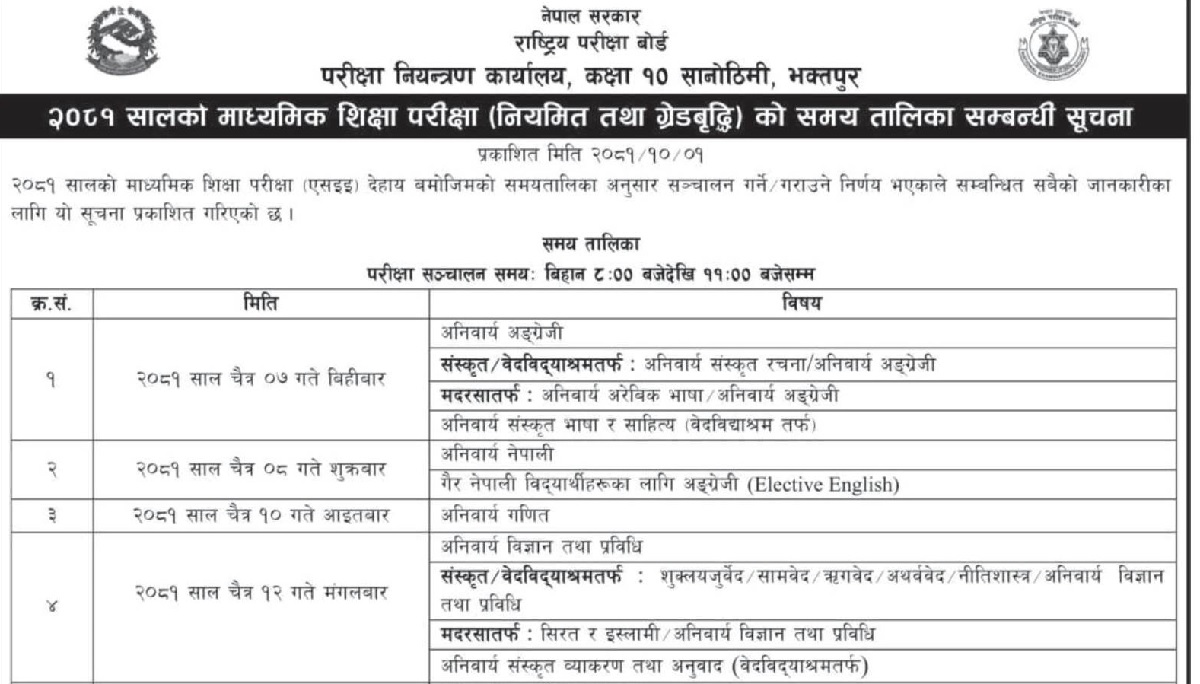
It is Algebra Formula collection. We have made this Algebra Formula collection for all level students. Hope this collection will be useful to all students.

Algebra Formula Collection

It is the era of information and technology. So students search each and every thing in internet. So to fulfill this demand we have made this Algebra Formula Collection.

Product Formula in Algebra

• a² – b² = (a – b)(a + b)
• (a + b)² = a² + 2ab + b²
• a² + b² = (a – b)² + 2ab
• (a – b)² = a² – 2ab + b²   

Square of three terms

• (a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc
• (a – b – c)² = a² + b² + c² – 2ab – 2ac + 2bc

Here we have next collection of algebra formula to find the cube of the sum of two terms. Such formulas are very common for basic level students. So if you are confuse regarding the formula at that moment just visit gbsnote.com.

• (a + b)³ = a³ + 3a²b + 3ab² + b³ ; (a + b)³ = a³ + b³ + 3ab(a + b)
• (a – b)³ = a³ – 3a²b + 3ab² – b³
• a³ – b³ = (a – b)(a² + ab + b²)
• a³ + b³ = (a + b)(a² – ab + b²)
• (a + b)³ = a³ + 3a²b + 3ab² + b³
• (a – b)³ = a³ – 3a²b + 3ab² – b³

Some Additional Formula in Algebra

• (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴)
• (a – b)⁴ = a⁴ – 4a³b + 6a²b² – 4ab³ + b⁴)
• a⁴ – b⁴ = (a – b)(a + b)(a² + b²)
• a⁵ – b⁵ = (a – b)(a⁴ + a³b + a²b² + ab³ + b⁴)

Algebra Formula Collection for Advance level

• If n is a natural number, aⁿ – bⁿ = (a – b)(a^n-1 + a^n-2b+…+ b^n-2a + b^n-1)
• If n is even (n = 2k), aⁿ + bⁿ = (a + b)(a^n-1 – a^n-2b +…+ b^n-2a – b^n-1)
• If n is odd (n = 2k + 1), aⁿ + bⁿ = (a + b)(a^n-1 – a^n-2b +…- b^n-2a + b^n-1)
• (a + b + c + …)² = a² + b² + c² + … + 2(ab + ac + bc + ….

<< Trigonometry Formula Collection >> Read More ……………………………

Here are the laws of indices. This law of indices is very important. So while solving the problem related to exponents it is highly used. Hence we suggest all the students to learn these formulas.

• Laws of Exponents
  (a^m)(aⁿ) = a^m+n
  (ab)^m = a^mb^m
  (a^m)ⁿ = a^mn
• Fractional Exponents
  a⁰ = 1

In this expression the base a itself can never be zero. Similarly while dividing the terms having the same base power will be subtracted.

So finally we request you to share this article to your students, friends and others if you really like it.