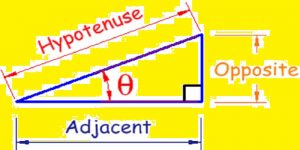
Formula is very important in Trigonometry. (from Greek trigōnon, “triangle” and metron, “measure”). It is a branch of mathematics that studies relationships involving lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. Trigonometry Formula plays key role in maths.
The 3rd-century astronomers first noted the relation of sides and angles. They noted that the lengths of the sides of a right-angle triangle and the angles between those sides have fixed relationships. Hence if at least the length of one side and the value of one angle is known, then all other angles and lengths can be determined algorithmically.
These calculations soon came to be defined as the trigonometric functions. And today are pervasive in both pure and applied mathematics. Fundamental methods of analysis such as the Fourier transform, for example, or the wave equation, use trigonometric functions to understand cyclical phenomena across many applications in fields as diverse as physics, mechanical and electrical engineering, music and acoustics, astronomy, ecology, and biology. Trigonometry is also the foundation of surveying.
Trigonometry is most simply associated with planar right-angle triangles. (each of which is a two-dimensional triangle with one angle equal to 90 degrees). The applicability to non-right-angle triangles exists. but, since any non-right-angle triangle (on a flat plane) can be bisected to create two right-angle triangles, most problems can be reduced to calculations on right-angle triangles.
Thus the majority of applications relate to right-angle triangles. One exception to this is spherical trigonometry, the study of triangles on spheres, surfaces of constant positive curvature, in elliptic geometry (a fundamental part of astronomy and navigation). Trigonometry on surfaces of negative curvature is part of hyperbolic geometry.
Trigonometry basics are often taught in schools, either as a separate course or as a part of a calculus course. If you have good knowledge of formula it the interesting subject.
List of formula in trigonometry
SinA. CosecA = 1
COSA. SECA = 1
TANA. COTA = 1
SIN2A + COS2A = 1
SEC2A – TAN2A = 1
COSEC2A – COT2A = 1
SIN (90 – A) = COSA
COS (180 + A) = – SINA.
COS (90 – A) = SINA.
TAN (90 – A) = TANA
SIN (90 + A) = COSA.
COS (90 + A) = -COSA.
TAN (90 + A) = -TANA.
SIN (180 + A) = -SINA.
TAN (180 + A) = TANA.
Trigonometry Formula
SIN (A + B) = SINA. COSB + COSA. SINB
COS (A +B) = COSA.COSB – SINA.SINB
TAN (A + B) = (TANA+TANB.)/(1-TANA.TANB)
COS (A – B) = COSA.COSB + SINA.SINB
TAN (A – B) = (TANA- TANB)/(1+ TANA.TANB)
COT (A + B) = (COTA.COTB – 1 )/(COTB+COTA)
COS2A = 2COS2A – 1
SIN2A = 2SINA.COSA
SIN2A =□((2TANA )/(1 + TAN.^2 A))
COS2A = COS2A – SIN2A
COS2A = 1 – 2SIN2A
SIN3A = 3SINA – 4SIN3A
COS3A = 4COS3A – 3COSA
Learning trigonometry is solely based on the concept of formula. Students are afraid on trigonometry. Learn formula properly for better performance in trigonometry. We also provide online help to solve mathematics problems. You can contact us in our Facebook page for online help and support.
Our Facebook page is gbsnote.com. Just like it and contact us online or offline. We help your kids to solve their problems while doing maths homework. Gbsnote if free and open site. It is open source of learning. Use it for your study.