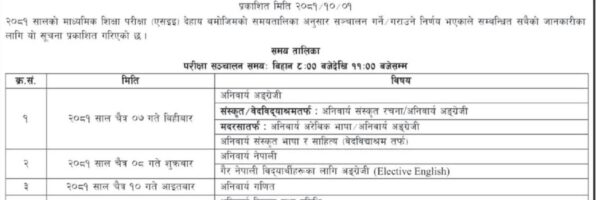
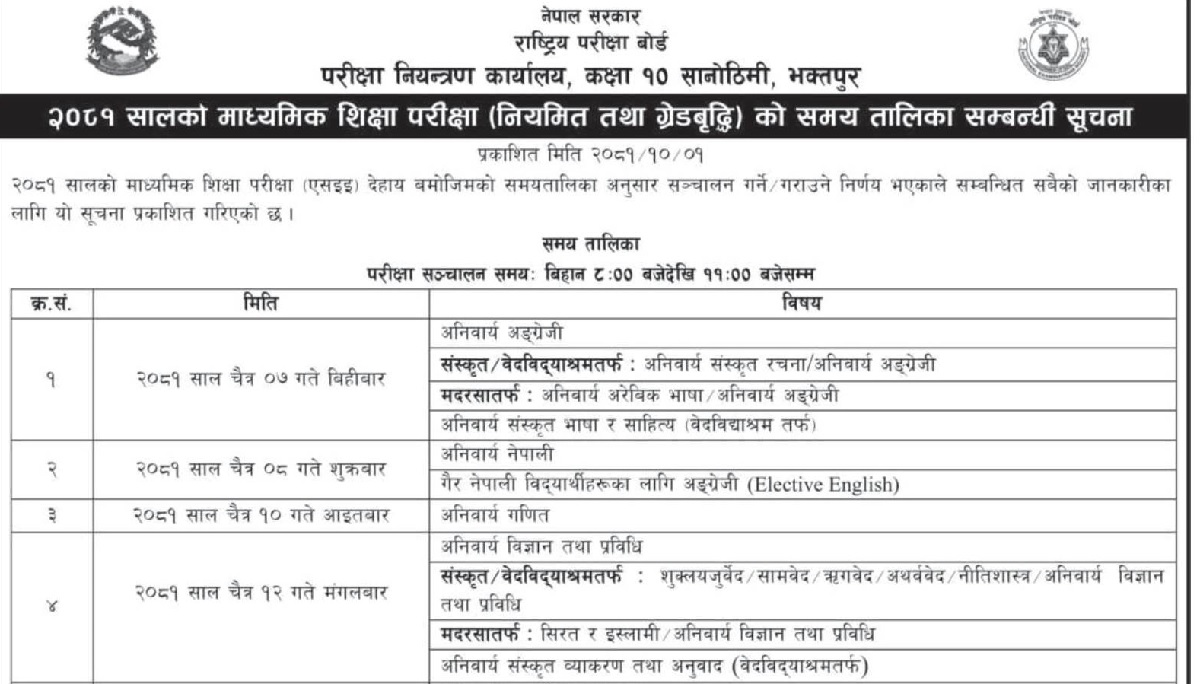
It is SLC Optional math questions. Opt maths is one of the choice in optional second group in SLC board of Nepal. Optional math is supposed to be little bit tough in comparison to other subjects in this group. Hope this collection will help the optional math students a lot to prepare their SLC exam.
1. a. If f(x)=3x+2 and g(x)=2x-1, find fog(x).
b. State remainder theorem. Use it to find the remainder when polynomial x^3-1 is divided by x-1.
2. a. Find the common ratio of a geometric sequence, whose first term is 2 and the third term is 242.
b. If A=[■(1&-1@3&-3)] and B=[■(2&-5@2&-5)] , show that AB is a null matrix.
3. a. If the matrix (■(2&-3@4&x)) has no inverse, find the value of x.
b. For what value of K are the lines 3x-4y+9=0 and Kx+3y-12=0 perpendicular to each other?
4. a. Find the angle between two lines represented by the equation 〖6x〗^2+5xy-〖6y〗^2=0 .
b. Find the equation of the circle having center (3, 6) and touching the x-axis.
5. a. Find the value of sin〖75〗^0 without using calculator.
b. Prove that: cot A/2-tan A/2=2cotA
6. a. Prove that: (1+cosθ+sinθ)/(1-cosθ+sinθ)=cot θ/2
b. Solve: 2sinθ-√3=0 (0^0≤θ≤〖90〗^0)
7. a. If |a ⃗ |=4√2,|b ⃗ |=4 and =〖45〗^0 , find the value of a ⃗.b ⃗.
b. In ABC, D and E divides AB and AC in the ratio 1:2 respectively, prove that DE ⃗=1/3 BC ⃗.
8. a. If r1 is the reflection about the y-axis and r2 is the rotation about -900 through origin, find the image of the point P(2, -4) under the combined transformation r1or2.
b. If P(a, b) is transformed by (■(0&-2@-2&0)) to P’ (-10, -8), find the value of and b.
SLC Optional Math Practice Questions
9. If g(x)=x/(2x-3) and g^(-1) (x)=g(x) , find the value of x.
10. Solve: x^3-〖6x〗^2+11x-6=0
11. The sum of the first ten terms of an AP is 50 and its fifth term is treble of the second term. Calculate the sum of the first twenty terms.
12. Find the maximum value of P=5x+3y under the following constraints.
2x+y≤20,2x+3y≤24 x≥0 y≥0
13. Solve by matrix method: 3x/2+2y=1, x/3-y/3=1
14. If P(2, 3) and R(-6, 5) are the two ends of the diagonal PR of a rhombus PQRS, find the equation of the other diagonal QS.
15. Find the single equation of a pair of straight lines passing through the origin and perpendicular to the line pairs represented by x^2-xy-〖2y〗^2=0 .
16. Find the center and radius of the circle having the equation 〖2x〗^2+〖2y〗^2-8x-12y+1=0
17. Prove that: 1/sin10-√3/cos10=4
Optional Math SLC Practice Question
22. A triangle with vertices A(1, 0), B(2, 1) and C(3, -1) is translated by T(1/2) and draw its image in the graph. Again its image is reflected by the line x=2 and draw its image in the same graph.
23. A square ABCD wit vertices A(2, 0), B(5, 1), C(4, 4) and D(1, 3) is mapped onto a parallelogram. A’B’C’D’ by a 2×2 matrix so that the vertices of the parallelogram are A'(2, 2), B'(7, 3), C'(12, -4) and D'(7, -5). Find the 2×2 transformation matrix.
24. Find the mean deviation from the mean and its coefficient:
Mark 0-10 10-20 20-30 30-40 40-50
No. of students 2 3 6 5 4
25. Find standard deviation and its coefficient.
Age in years 10 20 25 30 35 40
No. of persons 1 5 10 12 8 4